Improving transportation networks: Effects of population structure and decision-making policies
Web Annex of the original paper published in Scientific Reports
Federico Pablo Martí (1),*, Angel Sánchez (2), (3)
(1) Grupo de Sistemas Complejos en Ciencias Sociales (SCCS), Departamento de Economíıa, Universidad de Alcalá, Alcalá de Henares, Madrid, Spain
(2) Grupo Interdisciplinar de Sistemas Complejos (GISC), Departamento de Matemáaticas, and Institute UC3M-BS of Financial Big Data, Universidad Carlos III de Madrid, Leganés, Madrid, Spain
(3) Instituto de Biocomputación y Física de Sistemas Complejos (BIFI), Universidad de Zaragoza, Zaragoza, Aragón, Spain * federico.pablo@uah.es
|
|
Transportation networks are one of the fundamental tools for human society to work, more so in our globalized world. The importance of a correct, efficient design of a transportation network for a given region or country cannot be overstated. We here study how network design is affected by the geography of the towns or nuclei to be connected, and also by the decision process necessary to choose which connections should be improved (in a generic sense) first. We begin by establishing that Delaunay networks provide an efficient starting point for the network design and at the same time allow us to introduce a computationally amenable model. Subsequent improvements lead to decentralized designs in geographies where towns are more or less homogeneously distributed, whereas radial designs arise when there is a core-periphery distribution of nodes. We also show that optimization of Delaunay networks outperforms that of complete networks at a lower cost, by allowing for a proper selection of the links to improve. In closing, we draw conclusions relevant to policy making applied to designing transportation networks and point our how our study can be useful to identify mechanisms relevant to the historical development of a region. |
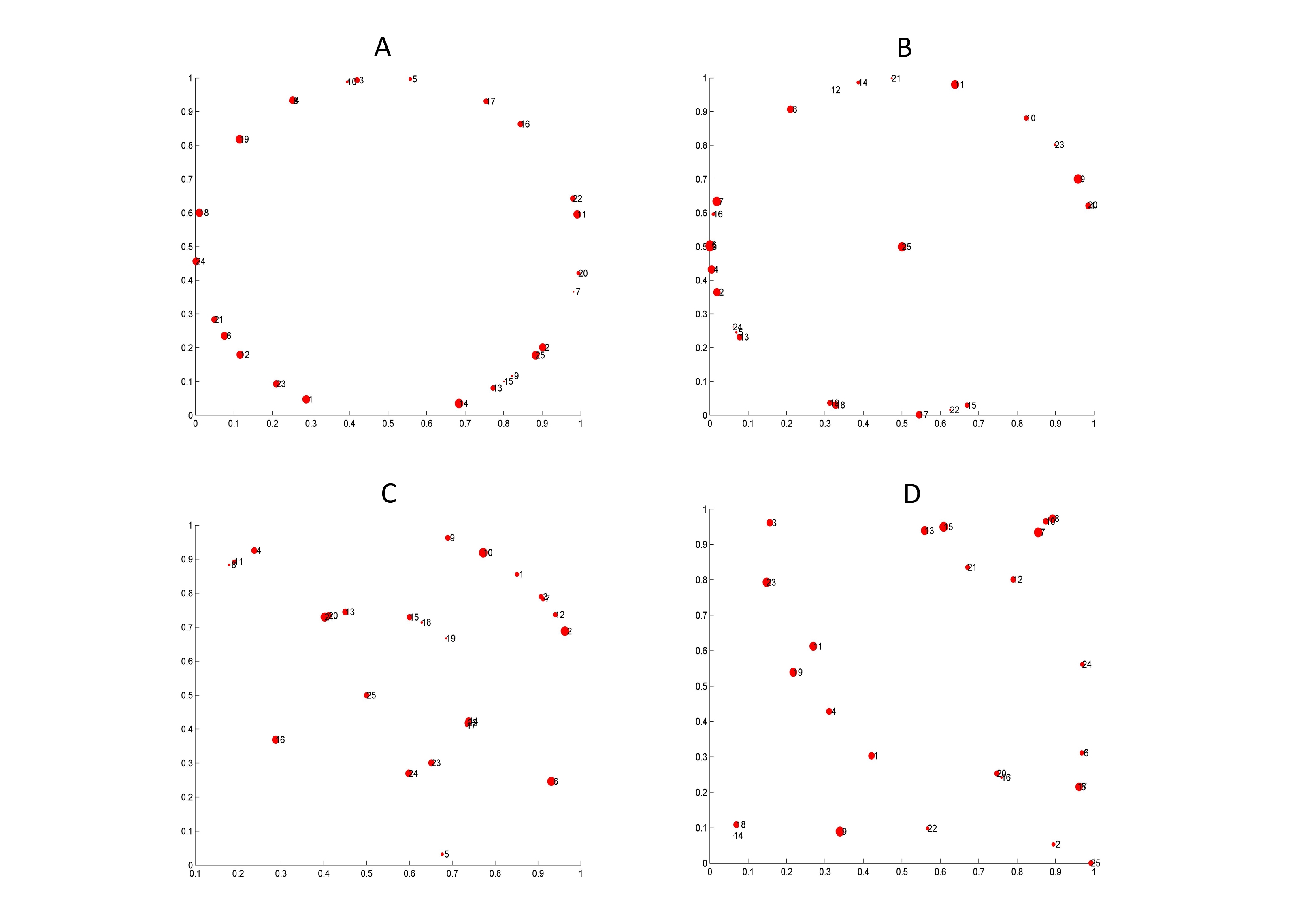
Representative examples of the different geographical distributions considered |
||
|---|---|---|
 |
||
| A: Circunference setup. B: Circunference and central point setup. C: Double circunference and central point setup. D: Random setup. | ||
Complete Networks vs. networks of Delaunay. Efficiency analysis |
||
| Comparison of the total cost of transport before improvements in the Delaunay and complete networks. | ||
Variations in decision-making processes. Number of nodes constant |
Variations in number of nodes. Decision-making processes constant |
|
|
|
Comparison of the evolution of total cost of transport after improvements in the Delaunay and complete networks.
|
|
| Ratio of total transport costs with Delaunay networks to complete networks.
|
||
| Comparison of the average size of the improved sections in Delaunay and complete networks.
|
||
| Comparison of section improvements effects on the total transport costs of Delaunay and complete networks.
|
||
The impact of the decision-making process on the networks |
||
Variations in decision-making processes. Number of nodes constant |
Variations in number of nodes. Decision-making processes constant |
|
| Example videos showing the sequential process of network enhancement.
|
||
| Effect of the section improvements on the Gini indices of the degree centrality .
|
||
| Effect of the section improvements on the Gini indices of the betweenness centrality. | ||
| Evolution of the difference between the Gini indices of betweenness centrality and those of degree centrality.
|
||

